생각만으로 컴퓨터에 글자 입력 가능해진다 & 컴퓨터의 탄생 & 왜 키보드는 ‘QWERTY’로 시작할까

“나는 유용한 일을 한 적이 없다. 나의 어떤 발견도 직접적이든 간접적이든, 좋든 나쁘든 상관없이 세상을 변화시키지 않았고 앞으로도 변화시키지 않을 것이다” -고드프리 해럴드 하디

많은 수학자가 자신의 연구가 현실에서 얼마나 쓸모 있을지에 대해 신경 쓰지 않을지도 모릅니다. 감히 추측하자면 독일 수학자 다비트 힐베르트나 미국 수학자 쿠르트 괴델도 하디와 비슷한 마음으로 논리학 연구에 임했을 것입니다.

그럼에도 많은 수학 연구는 뜻밖의 과정을 거쳐 공학이나 과학에서 아주 유용하게 사용됩니다. 괴델의 불완전성 정리도 그런 사례 중 하나입니다. 순수논리학에서만 다룰 것 같은 이 정리는 컴퓨터를 이 세상에 등장시켰습니다.

가상의 기계

시간을 잠시 거슬러 올라가 볼까요. 1928년 힐베르트는 수학의 발전을 위한 두 가지 과업을 제시합니다. 첫째는 참인 명제는 항상 증명 가능하다는 것을 보이는 것이고, 둘째는 어떤 명제가 주어졌을 때 이 명제가 증명 가능한지 아닌지를 판단하는 방법을 제시하는 것입니다. 수학 용어로 말하자면 첫 번째 목표는 수학의 완전성을, 두 번째 목표는 수학의 결정 가능성을 보이는 것입니다.

그러나 1931년 괴델의 불완전성 정리가 발표됨으로써 힐베르트의 첫 번째 목표는 불가능한 것으로 드러났습니다. 충격적인 발표에 자극을 받은 영국 수학자 막스 뉴먼은 자신의 강의에 불완전성 정리에 관한 내용을 포함하는데요. 이 수업의 수강생 중에는 앨런 튜링이라는 천재 학생이 있었습니다. 튜링은 영국 수학자로, 훗날 컴퓨터 공학 및 정보공학의 이론적 토대를 마련하는 인물이지요. 튜링은 괴델의 불완전성 정리에 깊은 감명을 받고, 어떻게 하면 괴델의 아이디어를 발전시켜 힐베르트의 두 번째 목표 또한 불가능하다는 것을 보일 수 있을지 궁리했어요. 이윽고 1936년 튜링은 수학의 결정 가능성마저 반증하는 논문을 발표하는데요. 이 논문은 아주 독창적인 아이디어를 사용합니다.

튜링은 어떤 가상의 기계를 상상했습니다. 현대 학자들은 이 기계를 ‘튜링 기계’라고 불러요. 튜링 기계는 주어진 일련의 절차(프로그램)을 수행하는 기계예요. 예를 들어 아래의 두 절차를 입력 받았을 때 튜링 기계의 출력 값은 다음과 같습니다.

튜링 기계의 동작은 단순하지만 튜링 기계는 상상 이상으로 강력합니다. 튜링 기계는 다른 기계가 풀 수 있는 문제라면 모두 풀 수 있거든요. 예를 들어 공학용 계산기로 ‘방정식’을 풀 수 있으므로, 튜링 기계도 가능합니다. 심지어 컴퓨터로 두는 체스도 튜링 기계로 둘 수 있습니다. 만약 튜링 기계가 해결할 수 없는 문제가 존재한다면 그것은 그 문제를 해결하는 기계적인 절차가 아예 존재하지 않음을 의미합니다.

튜링 기계가 못 푸는 문제

그렇다면 과연 튜링 기계가 해결할 수 없는 문제가 있을까요? 언뜻 보기에는 없을 듯합니다. 컴퓨터는 로켓도 쏘아 올리고, 바둑도 두고, 자동차도 운전합니다. 튜링 기계는 컴퓨터보다도 더 강력한 기계지요.

그러나 튜링 기계로도 풀 수 없는 문제가 있는데요, 바로 ‘정지 문제’입니다.

예를 들어 볼게요. 프로그램 Five는 입력 값이 5보다 작으면 정상적으로 종료하지만, 입력 값이 5 이상이면 영원히 종료하지 않습니다. 따라서 우리가 찾고자 하는 프로그램 P(x)는 Five와 4를 입력 받으면 참을 출력하고, Five와 6을 입력 받으면 거짓을 출력해야 합니다.

언뜻 보면 정지 문제는 체스 두기나 자동차 운전하기보다 훨씬 쉽게 느껴집니다. 그러나 튜링은 정지 문제를 푸는 프로그램은 논리적으로 존재할 수 없음을 보였습니다. 모든 명제가 증명 가능한지 기계적으로 판별하는 것이 가능하다면 ‘프로그램 P(x)는 정상적으로 종료한다’라는 명제 역시 P(x)가 정상적으로 종료하는지 판별할 수 있는데요. 정지 문제를 풀 수 없다는 사실은 수학이 결정 가능성을 지니지 않음을 의미합니다!

출처:Unsplash / clint patterson

PC, 스마트폰 태블릿에서 문자를 입력하려면 키보드가 필요합니다. 키보드는 크게 물리 키보드와 가상 키보드로 나뉘는데요. 형태의 차이일 뿐, 사용 목적과 키 배열은 유사해요. 물론 가상 키보드 중에 천지인, 나랏글처럼 독특한 배열도 있어요. 다만 모바일 기기에만 쓰이는 방식입니다. 우리가 주로 사용하는 키보드 배열은 ‘쿼티(qwerty)’입니다.

쿼티는 키보드 왼쪽 상단 키 배열이 Q-W-E-R-T-Y 순으로 나열돼 붙여진 명칭이에요. QWERTY를 그대로 읊어 ‘쿼티’로 발음하죠. 엄밀히 따지면 영문 키보드 배열 중 하나입니다. 쿼티가 영문 배열이긴 하지만, 현재 우리가 사용하는 키보드 형태에 상당한 영향을 줬다는 건 부정할 수 없습니다.

쿼티 배열은 언제 누가 개발했을까요. 이를 알기 위해선 키보드의 전신인 타자기의 역사를 되돌아봐야 합니다. 지금의 키보드 배열과 형태는 쿼티 방식 타자기로부터 많은 영향을 받았기 때문이죠. 모바일 기기 가상 키보드도 그렇습니다. 스마트폰 상용화 이후 휴대전화에서도 대중적으로 쓰이기 시작한 쿼티 배열은, 컴퓨터 키보드를 거의 그대로 옮겨온 형태입니다.

쿼티 배열, 누가 처음 만들었나?

출처:Smithsonianmag / Google Patents

기술은 언제나 사용하기 편한 방향으로 발전하기 마련입니다. 타자기도 이런 흐름 속에 있었어요. 최초의 타자기는 1700년대 발명됐는데요. 쿼티 배열이 모습을 드러내기 시작한 건 1800년대 중반부터입니다. 정치가이자 신문 발행인, 발명가인 미국인 크리스토퍼 래섬 숄즈(Christopher Latham Sholes)가 쿼티 배열의 시작을 알렸어요.

숄즈는 지난 1868년 동료들과 함께 개발한 타자기 특허를 확보했습니다. 당시 특허는 지금의 쿼티 배열과 거리가 멀었어요. 피아노와 비슷한 배열이었고, 28개 키가 전부였습니다. 쿼티와 유사한 배열은 그로부터 오랜 시간이 흐른 후였어요. 1873년, 숄즈는 타자기 상단 배열이 쿼티와 유사한 타자기 시제품을 선보였습니다.

숄즈는 1878년, 현재 쿼티 배열과 거의 같은 배열을 지닌 타자기를 개발하고, 특허로 등록했습니다. 해당 특허 내용은 지금도 찾아볼 수 있어요. 키는 총 네 줄로 배치돼 있는데요. 맨 윗줄에는 숫자 2~9, 붙임표(-), 쉼표(,) 키가, 그 아래에는 알파벳 키가 위치했습니다. 자세히 보면 QWERTY, ASDFG, ZXCVB 배열이 현재 키보드와 똑같습니다.

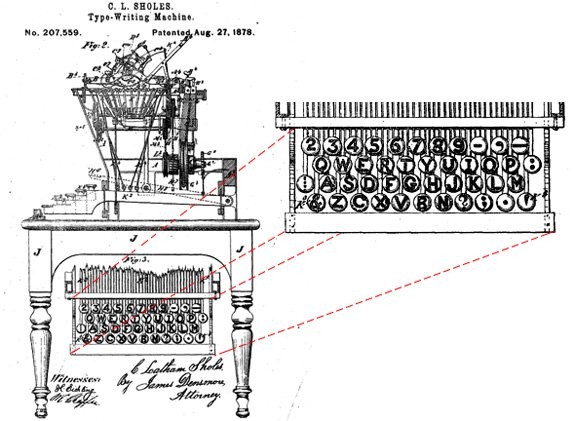
출처:Smithsonianmag / Google Patents

왜 하필 쿼티였나?
숄즈가 쿼티 배열 타자기를 개발한 이유는 불분명해요. 그래서 개발 배경을 두고 다양한 가설이 나왔는데요. 가장 유력한 설은 기계적 결함을 줄이기 위해 쿼티 배열을 택했다는 겁니다. 타자기는 자판을 누르면 잉크를 머금은 먹지를 내리쳐 종이에 문자를 입력하는 방식이었어요. 자판이 먹지에 닿고 돌아가는 시간이 충분해야 한다는 말이에요.

이런 이유로 종종 빠르게 타이핑하다 보면 자판이 올라가고 내려가는 사이에 얽혀서, 타자기가 고장 나는 문제가 발생했다고 합니다. 이에 숄츠가 의도적으로 자주 쓰이는 문자를 멀리 배치한 쿼티 배열을 만들었다는 가설이 유력해요. 꽤 그럴싸한 가설입니다. 실제 쿼티 배열은 T, H, E처럼 함께 자주 쓰이는 문자가 서로 떨어져 있어요.

하지만 예외도 있어요. 영어권에서 E, R은 굉장히 많이 사용되는 알파벳인데요. 쿼티 배열에서 두 문자는 바로 옆에 붙어있습니다.

크리스토퍼 래섬 숄즈 / 출처:Wikimedia Commons

쿼티가 대세가 된 이유는?
결론부터 말하면, 쿼티 배열이 널리 보급된 건 시장을 선점했기 때문입니다. 숄즈는 쿼티 배열 타자기를 판매하기 위해 총기 회사 레밍턴(Remington)과 손을 잡았어요. 당시 레밍턴은 남북전쟁 이후 총기 대신 다른 수입원이 필요했기에 숄즈의 타자기를 판매하기로 했죠. 결과는 성공적이었습니다. 1890년대까지 쿼티 배열 타자기 판매량은 10만대를 넘어섰어요.

쿼티 배열이 대세로 오른 중대한 사건이 하나 있습니다. 레밍턴을 비롯한 5개 타자기 제조업체의 합병이에요. 이들은 지난 1893년 합병을 마치고, 유니온 타이프라이터 컴퍼니(Union TypeWriter Company)를 설립했습니다. 그리고 쿼티 배열을 타자기 표준으로 채택했죠.

사람들은 익숙한 방식을 선호하기 마련입니다. 레밍턴은 이를 잘 알고 있었나 봅니다. 사용자들에게 값싼 비용으로 쿼티 배열 타자기 사용법을 배울 기회를 제공했어요. 자연스레 많은 이들이 쿼티 배열 타자기를 사용하기 시작했죠. 쿼티 배열 사용자가 늘어나고, 업계 표준이 되자 다른 업체들은 쿼티 배열을 뒤따를 수밖에 없게 됐습니다.

오늘날까지 쿼티 배열이 보편적으로 쓰이는 이유입니다. 이후 발명된 키보드는 타자기 배열을 그대로 계승했어요. 스마트폰 시대에 접어들면서, 쿼티 배열 가상 키보드가 널리 쓰이기 시작했고요.

출처:Unsplash / denny muller

쿼티 배열은 참 많은 것을 생각하게 합니다. 특별하지 않더라도 사용자와 시장을 빠르게 확보하면 성공할 수 있다는 전례를 남겼으니까요.

키보드 배열, 쿼티가 전부일까?
쿼티 배열이 가장 흔히 쓰이는 방식이라는 데는 반박의 여지가 없습니다. 허나 많이 사용된다고 해서 제일 편하다고 보긴 어려워요. 애초에 쿼티 배열은 사용성에 중점을 두고 만들어지지 않았으니까요. 이에 쿼티 키보드의 단점을 개선한 여러 키보드 배열이 등장했습니다. 물론 쿼티 배열의 아성에 미치지 못해 비주류로 전락했지만요.

쿼티 외 유명한 키보드 배열에는 드보락(Dvorak) 방식이 있어요. 워싱턴 대학 연구원이었던 어거스트 드보락(August Dvorak)이 1940년대 개발한 키보드 배열입니다. 드보락 배열은 쿼티 키보드의 문자 입력 방식을 개선했다고 해요. 드보락은 왼손 사용이 많은 쿼티 배열이 합리적이지 않다고 판단했어요. 사용자 대부분이 오른손잡이니까요.

출처:Wikimedia Commons

이런 이유로 만들어진 결과물이 드보락 배열입니다. 그러나 드보락 배열은 쿼티 배열을 뛰어넘지 못했습니다. 드보락은 자판 배열이 쿼티와 완전히 다른 방식이었는데요. 이미 쿼티 배열에 익숙해진 사용자들은 드보락 방식을 외면했어요. 쿼티보다 뛰어나다는 구체적인 근거도 부족했습니다. 지금도 드보락의 효용성을 두고 의견이 분분합니다.

쿼티 배열은 앞으로도 쭉 널리 쓰일 듯해요. 2000년대 들어서도 새로운 키보드 배열이 여럿 등장했지만 쿼티를 앞지르지 못했어요. 쿼티와 드보락의 장점을 합친 콜맥(CaleMak) 배열, 스마트폰·태블릿 등 모바일 기기에서 쿼티 키보드보다 더 빠르게 타이핑할 수 있는 칼큐(KALQ) 배열이 대표적이에요. 두 방식 모두 잘 쓰이지 않습니다.

국문 키보드 배열을 평정한 것은 무엇?

한글 최초 세벌식 타자기 / 출처:문화재청

여러분은 한글을 입력할 때 어떤 배열을 사용하고 계신가요. 아마 대부분 두벌식 배열을 쓰실 겁니다. 두벌식 키보드가 국내 표준이거든요. 두벌식 배열은 좌측에 자음, 우측에 모음을 배치해 직관적입니다. 사용하는 자판 수도 적어요. 영문 키보드와 자판과 정확히 일치하죠. 단 다른 배열에 비해 타이핑 속도가 느리다는 단점이 있어요.

두벌식, 세벌식, 네벌식 등 원래 한글 타자기 배열도 다양했는데요. 정부가 나서서 이를 하나로 정리했어요. 처음에는 정부 부처를 중심으로 네벌식이 흔히 쓰였습니다. 정부는 1980년대 들어 개인용 컴퓨터 보급이 확대되자, 타자기나 키보드 배열 통일에 나섰는데요. 네벌식을 폐기하고 지금의 두벌식을 표준으로 공표했어요.

두벌식 키보드 배열 / 출처:윈도우 화상 키보드

반드시 두벌식만 쓰라라는 법은 없죠. 일부 사용자들은 효율성이 좋다는 이유로 세벌식을 사용하곤 해요. 세벌식은 한글 제자 원리에 따라 초성, 중성, 종성을 따로 배치한 형태에요. 보다 빠른 타이핑이 가능하고, 정확성이 높다고 합니다. 하지만 드보락이 쿼티 배열을 넘어서지 못했듯, 세벌식도 주류가 되지 못했습니다. 제품을 구하기도 어렵고요.